Verbundenheit oder Vereinzelung, Zusammenhang oder Zersplitterung? Eine Illustration dieser fundamentalen Frage unserer Weltsicht fand ich einst an einem höchst unwahrscheinlichen, abstrakten Ort.
Die Mathematik kennt offene und abgeschlossene Mengen. Z.B. heißt das Intervall von 0 bis 1 incl. der 0 und 1 abgeschlossen und ohne diese Randpunkte offen. Ich erinnere mich noch genau, wie mir dieses Schulwissen eines Tages fraglich wurde: Müssten die beiden Mengenarten nicht umgekehrt heißen? Denn aus der sogenannten offenen Menge gibt es keinen Weg hinaus: Nehme ich eine beliebige Zahl ganz nah an der 1, z.B. die 0,999… mit 99 Neunen. Dann liegen zwischen dieser und der 1 immer noch unendlich viele weitere Zahlen: Die 0,999… mit 100, 1.000, Millionen Neunen. Was soll daran offen sein? Das Intervall kennt nur sich selbst – geschlossene Gesellschaft. Erst der Randpunkt, die 1, schließt auch an das Außen an, öffnet also das Intervall und verbindet es mit den Zahlen > 1! Und was für die 1 gilt, gilt natürlich für jede andere Zahl auf dem Zahlenstrahl auch, denn sie alle sind Rand für die beiden Mengen rechts und links von ihnen.
Was bedeutet das für die Frage nach Verbundenheit oder Vereinzelung? Wenn Randpunkte dieser oder jener Seite zugeschlagen werden und so Mengen abschließen, wie es die Mathematik will, dann muss man sich den Zahlenstrahl als eine Aneinanderreihung unendlich vieler unzusammenhängender Punkte vorstellen. Zahlenpulver, lauter Teile und kein Ganzes. Erst wenn Punkte Mengen füreinander öffnen und verbinden, wird der Zahlenstrahl ein zusammenhängendes Ganzes. Kann ich frei entscheiden, wie ich den Zahlenstrahl sehen will? Als „Zahlenpulver“ oder als einen verbundenen „Faden“? Ist die Entscheidung also beliebig, nur zwei Sichtweisen auf ein Gedankenspiel?
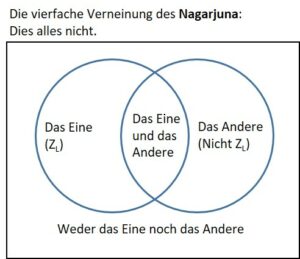
Mal sehen. Folgen wir der Vorstellung vom verbundenen Zahlenfaden weiter. Was bedeutet es, rein logisch, wenn sich der einzelne Punkt nicht als Rand dieser oder jener Seite zuweisen lässt? R sei der Randpunkt, ZL seien die Zahlen links von ihm und Nicht-ZL die Zahlen rechts. Dann gehört R, je nach Perspektive, zu allen der folgenden vier Mengen, und er ist somit Element von keiner von ihnen:
a) ZL, b) Nicht-ZL, c) ZL und Nicht-ZL und d) weder ZL noch Nicht-ZL. Für den Randpunkt in dieser Sicht gilt also die sogenannte vierfache Verneinung, das Tetralemma des Nagarjuna, ein buddhistischer Mönch aus dem 2. Jahrhundert.
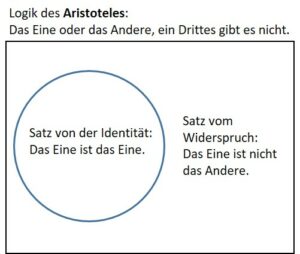
„Unsinn“, sagt die Logik des Aristoteles, verweist auf den Satz vom Widerspruch und verlangt R per Definition ZL oder Nicht-ZL zuzuschlagen. Nur so lassen sich klare und eindeutige Begriffe gewinnen.
Die Mathematik gehorcht und so heißt die Gewinnerseite abgeschlossen, die Verliererseite offen.
Doch „Heureka“, ruft die Ontologie, „genauso ambigue aber verbunden geht es bei mir zu. Ich habe die definitorische Gewaltherrschaft der Logik satt!“ Denn ist es nicht so in der Welt der wirklichen Dinge: Zwei Zimmer und eine Wand dazwischen. Zwei Zellen und eine Membran dazwischen. Egal was. Es ist konstitutiv für Wände oder Membranen etc., dass sie die Zimmer, Zellen unterscheiden und verbinden. Zugleich, in Einem. Das ist es, was sie ausmacht, ihr Wesen. Es ist sinnlos, per Definition die Wand einem der Zimmer zuschlagen zu wollen.
So sind die Dinge der Wirklichkeit beschaffen. Ziehen wir ein Einzelnes heraus, um es zu untersuchen, betrachten wir eine Abstraktion. Erst wenn wir es (oder auch uns selber) wieder einsetzen in alle Zusammenhänge, ist es da als etwas wirklich Seiendes.
Das ist es, was ich sagen wollte: Es gibt ganz wunderbar sinnvollen Unsinn wie den miteinander verbundener Individuen. Und der ist der Realität näher als alles, was in logisch vereindeutigten Begriffen und Aussagen gefasst werden kann. Danach gilt es, Ausschau zu halten.
W.D.
Hier geht es zum vorangegangenen Beitrag.
Hier geht es zur Webseite des Arbeitskreises Glaube und Naturwissenschaft.




Interessante Überlegungen, lieber Herr Dressler, allerdings nur für den Bereich der Mathematik.
In Kürze drei Überlegungen dazu:
Die Wirklicheit kennt keine beliebig kleine Aufteilung bis an den mathematisch definierbaren “Rand” einer Menge. Die “Kleinheit” ist begrenzt durch das Wirkungsquantum, räumlich und energetisch.
Zum anderen gibt es physikalisch keine “geschlossen” Räume oder Zimmer. Einerseits haben sie nicht selten mehr als eine Tür, andererseits sind sie auch bei geschlossenen Türen mit der Umgebung verbunden. Gefängisinsassen haben eine große Phantasie, diesen Umstand auch bei Einzelhaft in der Isolierzelle zu nutzen: entweder direkt physikalisch, oder durch die zahlreichen Möglichkeiten der Information, also Zeichen.
Schließlich ist auch physikalisch gesehen kein Raum je geschlossen, permeabel für zahlreiche Arten von Wellen.
Herzlichst,
Klaus Dietrich Wachlin
Lieber Herr Wachlin, wie schön auf diesem Weg nach all der Zeit wieder etwas von Ihnen zu hören!
Ich finde, Sie haben den Punkt, um den es mir geht, mit guten Beispielen ergänzt: Die Wirklichkeit ist nicht ganz so, wie es die mathematischen Modelle gelegentlich nahelegen, die sie beschreiben sollen. Logische Entitäten sind in sich geschlossen. Ontologische Entitäten immer verbunden.
Selbst, wenn die Tür zu ist – im Gefängnis – muss für Menschen die Verbundenheit nicht aufhören.
Freilich gibt es auch das umgekehrte Beispiel: Ein Einzelner kann sich in den Massen einer Großstadt vollkommen einsam und isoliert vorkommen. Wer sich so als vereinzeltes Sandkorn in einem unverbundenen Universum sieht, mag in meinen Gedanken eine Wink finden, es könne auch anders sein.